Metaheuristics - an Intuitive Package for Global Optimization

Author: Jesús-Adolfo Mejía-de-Dios (@jmejia8)

High-performance algorithms for optimization coded purely in a high-performance language.

Introduction

Optimization is one of the most common tasks in the scientific and industrial field but real-world problems require high-performance algorithms to optimize non-differentiable, non-convex, discontinuous functions. Different metaheuristics algorithms have been proposed to solve optimization problems but without strong assumptions about the objective function.

This package implements state-of-the-art metaheuristics algorithms for global optimization. The package aims to provide easy-to-use (and fast) metaheuristics for numerical global optimization.

Installation

Open the Julia (Julia 1.1 or Later) REPL and press ] to open the Pkg prompt. To add this package, use the add command:

pkg> add Metaheuristics

Or, equivalently, via the Pkg API:

julia> import Pkg; Pkg.add("Metaheuristics")

Quick Start

Assume you want to solve the following minimization problem.

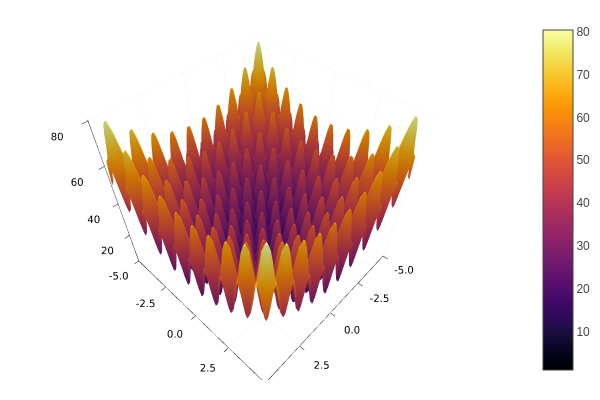
Minimize:

\[f(x) = 10D + \sum_{i=1}^{D} x_i^2 - 10\cos(2\pi x_i)\]

where $x\in[-5, 5]^{D}$, i.e., $-5 \leq x_i \leq 5$ for $i=1,\ldots,D$. $D$ is the dimension number, assume $D=10$.

Solution

Firstly, import the Metaheuristics package:

using Metaheuristics

Code the objective function:

f(x) = 10length(x) + sum( x.^2 - 10cos.(2π*x)  )

Instantiate the bounds:

D = 10
bounds = boxconstraints(lb = -5ones(D), ub = 5ones(D))

Also, bounds can be a $2\times 10$ Matrix where the first row corresponds to the lower bounds whilst the second row corresponds to the upper bounds.

Approximate the optimum using the function optimize.

result = optimize(f, bounds)

Optimization Result
===================
  Iteration:       883
  Minimum:         0.994959
  Minimizer:       [-4.48345e-09, -9.30599e-10, 3.25831e-10, …, -0.994959]
  Function calls:  61810
  Total time:      0.3276 s
  Stop reason:     Due to Convergence Termination criterion.

Optimize returns a State datatype which contains some information about the approximation. For instance, you may use mainly two functions to obtain such an approximation.

minimum(result)

0.9949590570932969

minimizer(result)

10-element Vector{Float64}:
 -4.4834466353035e-9
 -9.305989054639169e-10
  3.258305882527824e-10
  1.2886522823709618e-9
 -2.8635734772523426e-9
 -5.632279074993702e-10
 -3.368283468758625e-9
 -1.0454825577878258e-9
 -4.519765429079066e-9
 -0.9949586384993971

Contents

• Examples
• • Single-Objective Optimization
  • Constrained Optimization
  • Multiobjective Optimization
  • Bilevel Optimization
  • Decision-Making
  • Providing Initial Solutions
  • Batch Evaluation
  • Modifying an Existing Metaheuristic
  • Restarting search
• Algorithms
• • Evolutionary Centers Algorithm
  • Differential Evolution
  • Particle Swarm Optimization
  • Artificial Bee Colony
  • MOEA/D-DE
  • Gravitational Search Algorithm
  • Simulated Annealing
  • Whale Optimization Algorithm
  • NSGA-II
  • NSGA-III
  • SMS-EMOA
  • SPEA2
  • BCA
  • MCCGA
  • GA
  • CCMO
  • $\varepsilon$DE
  • BRKGA
• Problems
• • Box-constrained Optimization
  • Constrained Optimization
  • Multi-objective Optimization
• Performance Indicators
• • Generational Distance
  • Generational Distance Plus
  • Inverted Generational Distance
  • Inverted Generational Distance Plus
  • Spacing Indicator
  • Covering Indicator ($C$-metric)
  • Hypervolume
  • $\Delta_p$ (Delta $p$)
  • $\varepsilon$-Indicator
• Multi-Criteria Decision-Making
• • JMcDM
  • Region of Interest Archiving
  • Compromise Programming
• Visualization
• • Population Distribution
  • Convergence
  • Animate convergence
  • Pareto Front
  • Live Plotting
• API References
• • Methods for Solutions/Individuals
  • Variation
  • Population
  • Stopping Criteria
  • Sampling

Related packages

• Evolutionary.jl: Genetic algorithms, "Evolution" Strategies, among others.
• GeneticAlgorithms.jl: Genetic Algorithms
• BlackBoxOptim.jl: Optimizers for black-box optimization (no information about the objective function).
• NODAL.jl: Stochastic Local Search methods, such as Simulated Annealing and Tabu Search.
• Other Packages.

How to cite?

Please cite the package using the bibtex entry

@article{metaheuristics2022, 
  doi = {10.21105/joss.04723}, 
  url = {https://doi.org/10.21105/joss.04723}, 
  year = {2022}, 
  publisher = {The Open Journal}, 
  volume = {7}, 
  number = {78}, 
  pages = {4723}, 
  author = {Jesús-Adolfo Mejía-de-Dios and Efrén Mezura-Montes}, 
  title = {Metaheuristics: A Julia Package for Single- and Multi-Objective Optimization}, 
 journal = {Journal of Open Source Software} }

or the citation string

Mejía-de-Dios et al., (2022). Metaheuristics: A Julia Package for Single- and Multi-Objective Optimization. Journal of Open Source Software, 7(78), 4723, https://doi.org/10.21105/joss.04723

in your scientific paper if you use Metaheristics.jl.

Acknowledgments

Jesús Mejía acknowledges support from the Mexican Council for Science and Technology (CONACyT) through a scholarship to pursue graduate studies at the University of Veracruz, MEXICO. This allowed the development of Metaheuristics.jl from August 2018 to July 2022.