Edit on GitHub

Multi-Criteria Decision-Making

A set of Multi-Criteria Decision Making (MCDM) methods is available in Metaheuristics.jl.

Maximization or Minimization

Here, minimization is always assumed.

Firstly, it is recommended to read the details of the following two functions.

Metaheuristics.decisionmaking — Function
decisionmaking(fs, w, method)

Perform selected method for a given fs and weight vector(s) and return the indices indicating the best alternative(s). Here, fs can be a set of non-dominated solutions (population) or a State.

source
Metaheuristics.best_alternative — Function
best_alternative(res, w, method)

Perform McDM using results from metaheuristic and return best alternative in res.population.

Example

julia> f, bounds, _ = Metaheuristics.TestProblems.ZDT1();

julia> res = optimize(f, bounds, NSGA2());

julia> best_sol = best_alternative(res, [0.5, 0.5], TopsisMethod())
(f = [0.32301132058506055, 0.43208538139854685], g = [0.0], h = [0.0], x = [3.230e-01, 1.919e-04, …, 1.353e-04])
source
best_alternative(population, w, method)

Perform method and return the best alternative(s) in population.

source

Currently available methods are listed in the following table.

MethodStrategiesPreferencesDependency
CompromiseProgrammingSW/D
ROIArchivingMD
ArasMethodSWJMcDM
CocosoMethodSWJMcDM
CodasMethodSWJMcDM
CoprasMethodSWJMcDM
EdasMethodSWJMcDM
ElectreMethodMWJMcDM
GreyMethodSWJMcDM
MabacMethodSWJMcDM
MaircaMethodSWJMcDM
MooraMethodSWJMcDM
SawMethodSWJMcDM
TopsisMethodSWJMcDM
VikorMethodSWJMcDM
WPMMethodSWJMcDM
WaspasMethodSWJMcDM
MarcosMethodSWJMcDM
ROVMethodSWJMcDM

A Method can suggest Single (S) or Multiple (M) Strategies. Also, Methods can represent Preferences by using weight vectors (W), reference directions (D) or reference points (P).

JMcDM

JMcDM is a package for MCDM developed by (Satman et al., 2021). Many methods have been implemented there, and many of them have been interfaced here.

The main method to use JMcDM within Metaheuristics is described as follows.

mcdm(data, w, method)

Perform selected method for a given data and weight vector w. Here, data can be a set of non-dominated solutions (population), a State or a decision Matrix.

Also, method can be selected from JMcDM package.

Supported MCDM methods:

  • ArasMethod
  • CocosoMethod
  • CodasMethod
  • CoprasMethod
  • EdasMethod
  • ElectreMethod
  • GreyMethod
  • MabacMethod
  • MaircaMethod
  • MooraMethod
  • SawMethod
  • TopsisMethod (default method)
  • VikorMethod
  • WPMMethod
  • WaspasMethod
  • MarcosMethod
  • ROVMethod

See the JMcDM documentation for more details about the methods.

Example 1:

Performing MCDM using a population.

julia> _, _, population = Metaheuristics.TestProblems.ZDT1();

julia> dm = mcdm(population, [0.5, 0.5], TopsisMethod());

julia> population[dm.bestIndex]
(f = [0.5353535353535354, 0.2683214262030523], g = [0.0], h = [0.0], x = [5.354e-01, 0.000e+00, …, 0.000e+00])

Example 2:

Performing MCDM using results from metaheuristic.

julia> f, bounds, _ = Metaheuristics.TestProblems.ZDT1();

julia> res = optimize(f, bounds, NSGA2());

julia> dm = mcdm(res, [0.5, 0.5], TopsisMethod());

julia> res.population[dm.bestIndex]
(f = [0.32301132058506055, 0.43208538139854685], g = [0.0], h = [0.0], x = [3.230e-01, 1.919e-04, …, 1.353e-04])

Selecting best alternative

best_alternative(res, w, method)

Perform McDM using results from metaheuristic and return the best alternative in res.population.

julia> f, bounds, _ = Metaheuristics.TestProblems.ZDT1();

julia> res = optimize(f, bounds, NSGA2());

julia> best_sol = best_alternative(res, [0.5, 0.5], TopsisMethod())
(f = [0.32301132058506055, 0.43208538139854685], g = [0.0], h = [0.0], x = [3.230e-01, 1.919e-04, …, 1.353e-04])

Region of Interest Archiving

ROIArchiving uses a set of reference directions to determine the areas of interest of the Pareto Front and a set of thresholds associated with each component from the reference directions, which determine the boundaries of the area of interest being covered. See (de-la-Cruz-Martínez et al., 2022).

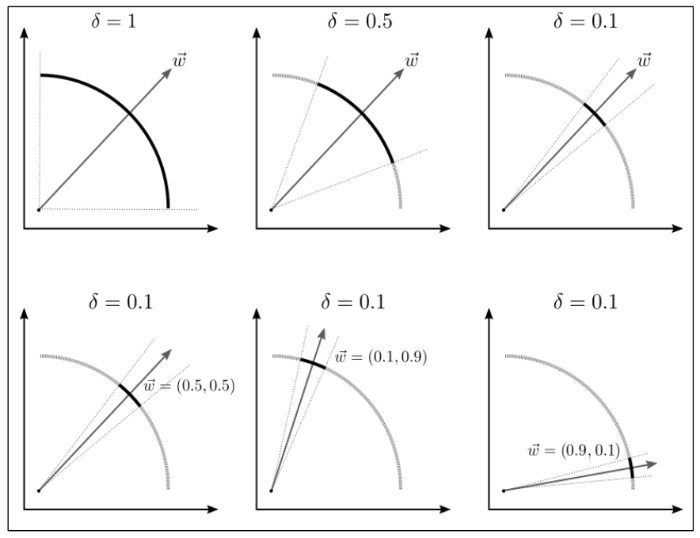
Parameters for the Region of Interest Archiving method

Metaheuristics.ROIArchiving — Type
ROIArchiving(δ_w)

It can be used as a posteriori decision-making criteria applied to the Pareto front found by a metaheuristic when solved a constrained multi-objective problem.

ROIArchiving can handle multiple weight points and corresponding thresholds δ_w. Note 0 <= δ_w[i] <= 1 indicates the size of region of interest, e.g., δ_w[i] = 0.51 means that you want 51% of the Pareto front solutions close to w[i].

Example

julia> f, bounds, pf = Metaheuristics.TestProblems.ZDT1();

julia> res = optimize(f, bounds, NSGA2()); # find Pareto front

julia> ws = [0.1 0.9; 0.9 0.1]; # weight points by rows.

julia> # 10% of solutions closest to the corresponding w[i]
julia> method = ROIArchiving([0.1, 0.1]); # 10% of solutions closest to the corresponding w[i].

julia> subpop = best_alternative(res, ws, method)
          ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀F space⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ 
          ┌────────────────────────────────────────┐ 
      0.9 │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⢣⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⢣⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⠀⠑⡄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⠀⠀⠈⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
   f₂     │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠉⠁⠠⠄⠀⠀⠀⠀⠀│ 
        0 │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠑⠂⠀⠀│ 
          └────────────────────────────────────────┘ 
          ⠀0⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀1⠀ 
        ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀f₁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
julia> res.population # all solutions
          ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀F space⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ 
          ┌────────────────────────────────────────┐ 
      1.1 │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⡃⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠘⡄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠈⢆⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⠈⠑⡄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⠀⠀⠈⠢⣄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
   f₂     │⠀⠀⠀⠀⠀⠀⠈⠓⢢⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠒⢄⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠑⠆⣄⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠐⠠⣀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠉⠂⠢⠄⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠙⠰⠤⣀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ 
          │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠁⠑⠒⠄⢀⡀⠀⠀⠀⠀⠀│ 
        0 │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠒⠤⠄⣀│ 
          └────────────────────────────────────────┘ 
          ⠀0⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀1⠀ 
          ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀f₁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
source

Compromise Programming

More information about Compromise Programming can be found in (Ringuest, 1992)

Metaheuristics.CompromiseProgramming — Type
CompromiseProgramming(scalarizing)

Perform compromise programming by using the scalarizing function provided. Current implemented scalarizing function are

  • WeightedSum
  • Tchebysheff
  • AchievementScalarization.

Example

julia> f, bounds, pf = Metaheuristics.TestProblems.ZDT1();

julia> res = optimize(f, bounds, NSGA2());

julia> w = [0.5, 0.5];

julia> sol = best_alternative(res, w, CompromiseProgramming(Tchebysheff()))
(f = [0.38493217206706115, 0.38037042164979956], g = [0.0], h = [0.0], x = [3.849e-01, 7.731e-06, …, 2.362e-07])

julia> sol = best_alternative(res, w, CompromiseProgramming(WeightedSum()))
(f = [0.2546059308425166, 0.4958366970021401], g = [0.0], h = [0.0], x = [2.546e-01, 2.929e-06, …, 2.224e-07])

julia> sol = best_alternative(res, w, CompromiseProgramming(AchievementScalarization()))
(f = [0.38493217206706115, 0.38037042164979956], g = [0.0], h = [0.0], x = [3.849e-01, 7.731e-06, …, 2.362e-07])

julia> idx = decisionmaking(res, w, CompromiseProgramming(Tchebysheff()))
3
source